Polynomials

The definition

$p(x) = a_n x^n + a_{n-1} x^{n-1} + … + a_1 x + a_0$

where $a_i$ are the coefficients of the polynomial and $x$ is the variable. The degree of the polynomial is $n$ and the coefficients can be real or complex numbers. The polynomial can be evaluated at a specific value of $x$ by substituting that value into the equation and performing the arithmetic operations.

Types of polynomials

• Constant polynomial: A polynomial of degree 0, e.g., $p(x) = 5$.
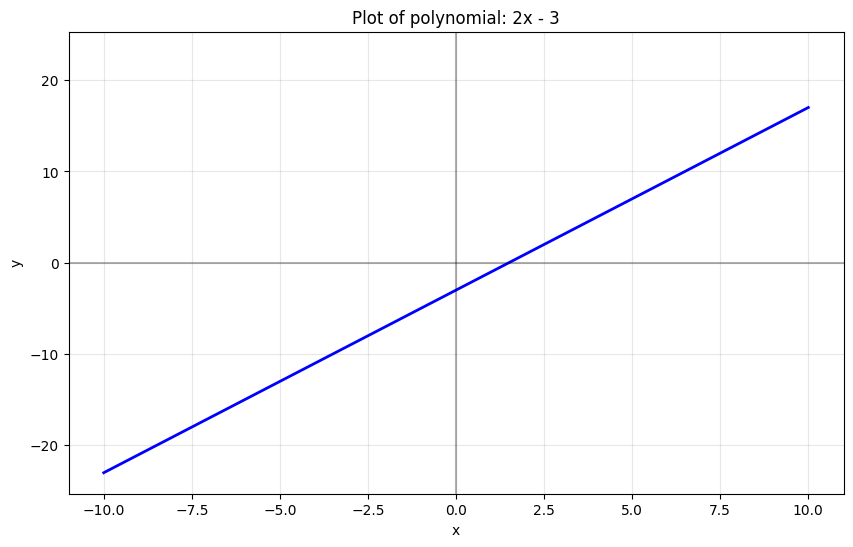
• Linear polynomial: A polynomial of degree 1, e.g., $p(x) = 2x + 3$.
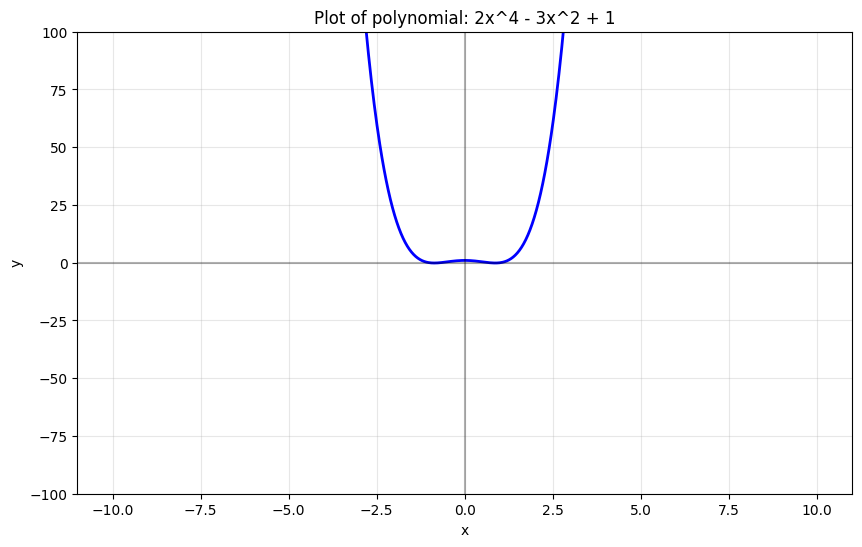
• Quadratic polynomial: A polynomial of degree 2, e.g., $p(x) = x^2 + 2x + 1$.
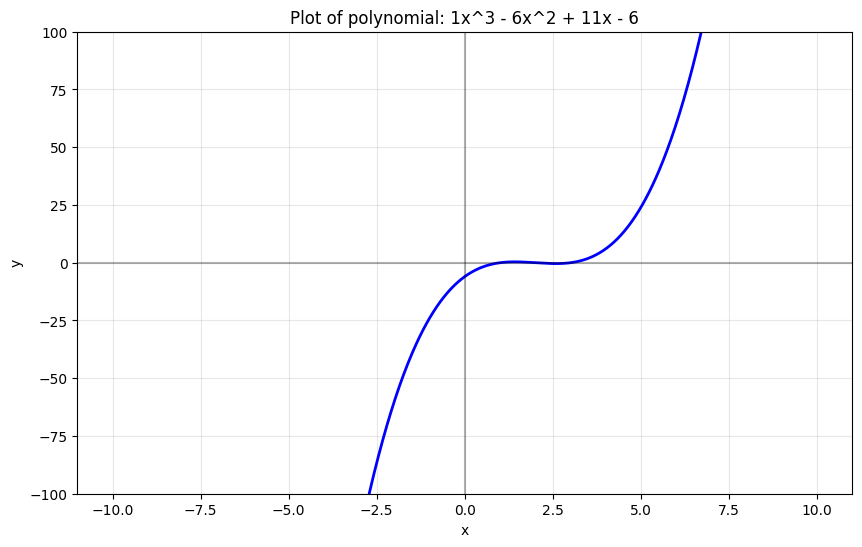
• Cubic polynomial: A polynomial of degree 3, e.g., $p(x) = x^3 + 2x^2 + 3x + 4$.

Intuition

A polynomial is like a cycle with gears. It can transform on peddle to a linear displacement. i.e. A polynomial is like transformer that can transform a simple input into a higher and more complex output. Something what the gears in the cycle does. It converts the simple peddling into higher speed in linear motion.

Polynomials are like machines that does this magic. And the magic is coded as a function of the independent variable. The output is the dependent variable.