Long Short Term Memory Networks (LSTM)

Why LSTMs - Long Short Term Memory Networks?

Disadvantages of RNNs

Vanishing gradient problem

Each state of the RNN is given by the $tanh$ activation function as follows :

\[h_t = tanh(Wh_{t-1} + Ux_t + b)\]

Typically the $-1 <= tanh <= 1$ This forces the recurrent activations to be bounded, preventing large eigenvalues. During backward propagation, gradients are computed as follows : \(\frac{\partial L}{\partial h_t} = W^T \cdot \frac{\partial L}{\partial h_{t+1}}\)

This means that the gradient at earlier time steps depends on multiplying $W^T$ multiple times.

\[\frac{\partial L}{\partial h_0} = (W^T)^T \cdot (W^T)^{T-1} \cdot \cdot \cdot (W^T) \frac{\partial L}{\partial h_t}\]

if largest eigenvalue of W, denoted by $\lambda_{max}$ is less than 1: \(\lambda_{max}^T (W) < 1\)

then each multiplication shrinks the gradient exponentially, leading to vanishing gradient problem.

\[(W^T)^T ≈ 0 \ as \ T → ∞\]

Limitation on context size

RNNs have a limitation on the context size they can remember. This is because the hidden state at time $t$ is a function of the hidden state at time $t-1$ and the input at time $t$. This means that the hidden state at time $t$ can only remember information from the previous time steps.

One of the major advantage of the RNNs had been that they have the ability to connect previous information to the present task, such as previous video frames might inform the understanding of the present frame.

Sometimes, we need to look back to the recent past to perform the present task. For example, say a language model trying to predict the next word. As per markov assumption , just knowing the probability of the previous word is enough to predict the next word. In such cases where the gap between the relevant information and the point where it is needed is small, RNNs can learn to use the past information. But when this gap increases, RNNs fail to learn to connect the information. Something like this, where the information from say previous sentence or previous paragraph is needed! For example in the illustration below, when 100th state needs input from 0th state, RNNs fail to learn this.

The LSTM - Long short term memory neural networks help to solve these two problems in RNNs.

LSTM architecture

LSTMs - Long short term memory networks are a special kind of RNN, capable of learning long-term dependencies. They were introduced by Hochreiter & Schmidhuber in 1997

The repeating module in a standard RNN contains a single layer

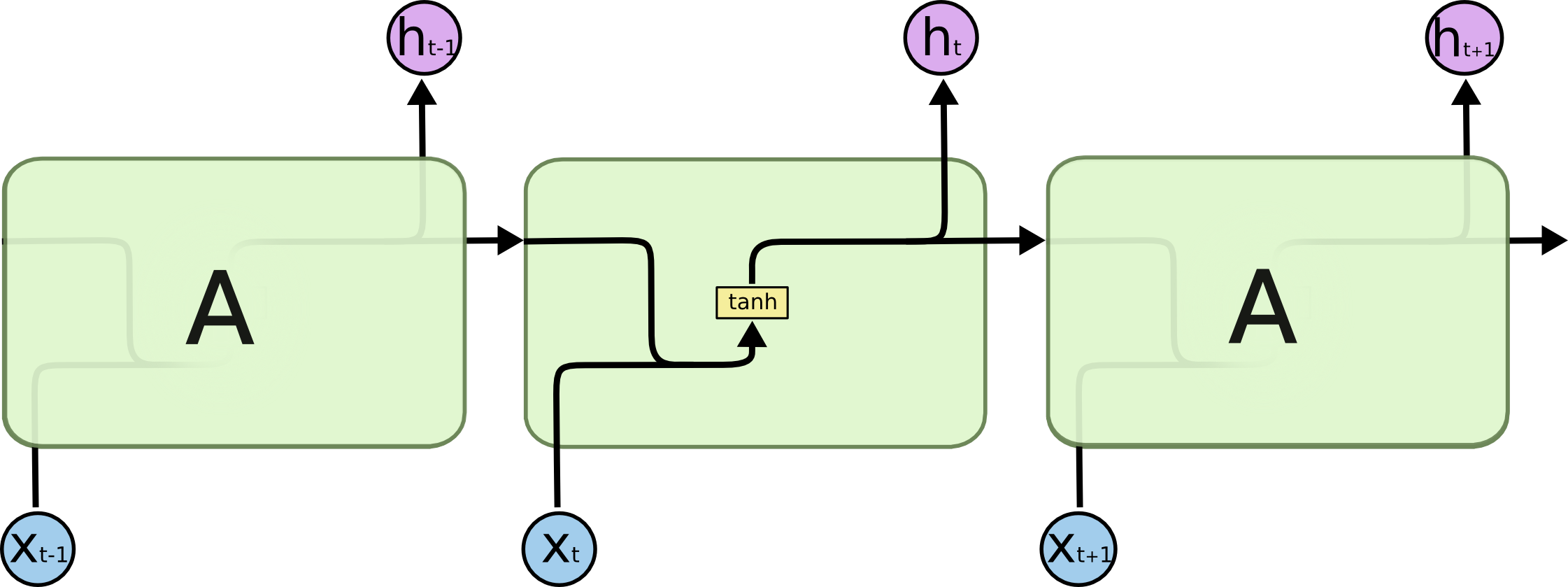
The repeating module in an LSTM contains four interacting layers

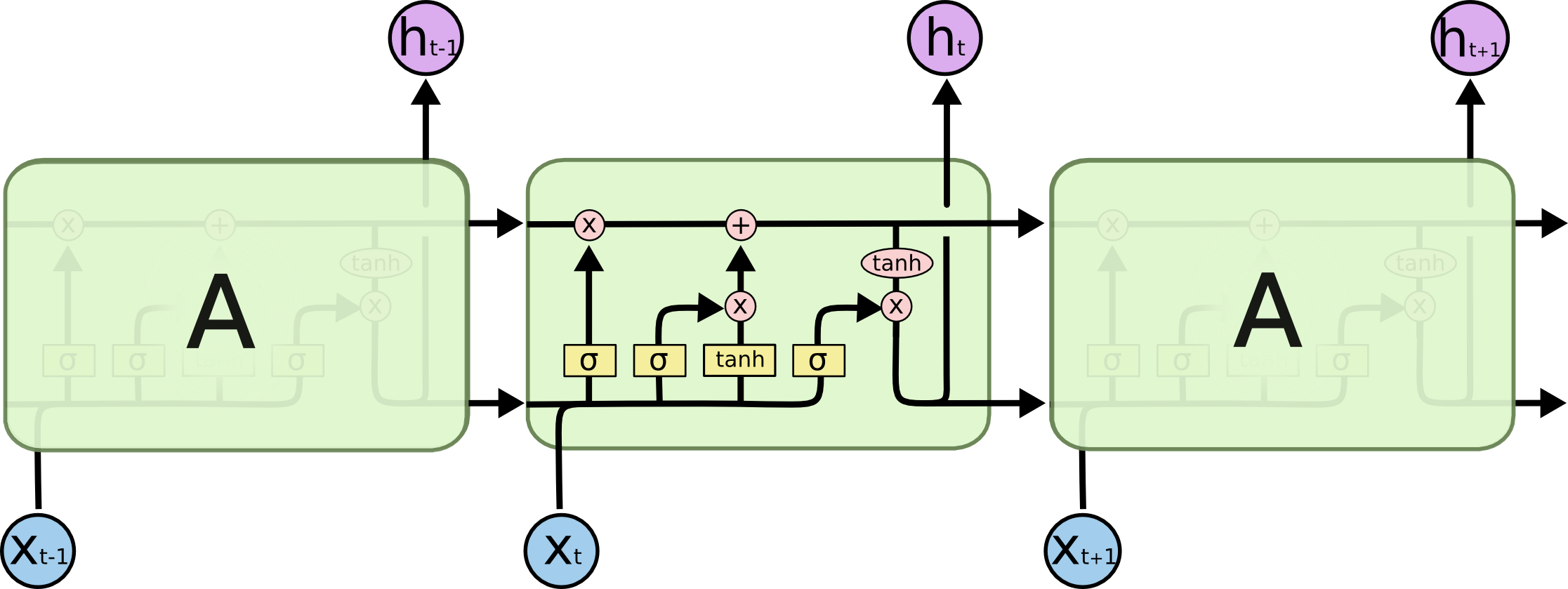
In the above diagram, each line carries an entire vector, from the output of one node to the inputs of others. The pink circles represent pointwise operations, like vector addition, while the yellow boxes are learned neural network layers. Lines merging denote concatenation, while a line forking denote its content being copied and the copies going to different locations.

Gates in LSTM

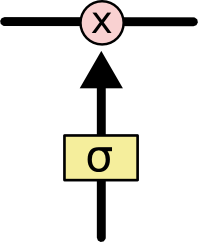
Gates are a way to optionally let information through. They are composed out of sigmoid neural net layer and a point-wise multiplication operation. The sigmoid layer outputs a number between 0 and 1, describing how much of each component should be let through. A 0 represents “let nothing through,” while a 1 represents “let everything through!”

1. Cell State

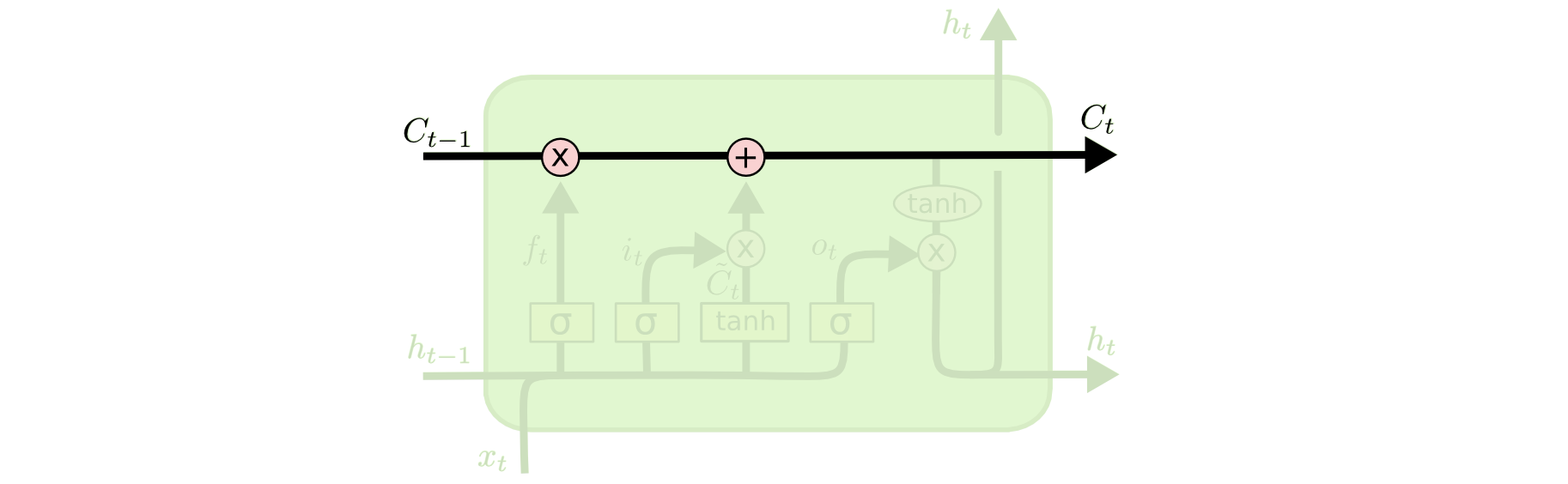
The key to LSTMs is the cell state, the horizontal line running through the top of the diagram.

The cell state is kind of like a conveyor belt. It runs straight down the entire chain, with only some minor linear interactions. It’s very easy for information to just flow along it unchanged.

Note that this is not a trainable neural network. Rather it is just a static memory that runs through the entire chain.

2. Forget obsolete data gate layer

This is a trainable neural network layer which uses an activation function as a sigmoid, working towards deleting an existing information in the cell state. The sigmoid layer outputs a number between 0 and 1, describing how much of each component of the cell state should be forgotten. It looks at $h_{t−1}$ and $x_t$, and outputs a number between 0 and 1 for each number in the cell state $C_{t−1}$. A 1 represents “completely keep this” while a 0 represents “completely get rid of this.” For example, in a language model, the cell state might include the gender of the present subject, so that the correct pronouns can be used. When we see a new subject, we want to forget the gender of the old subject.

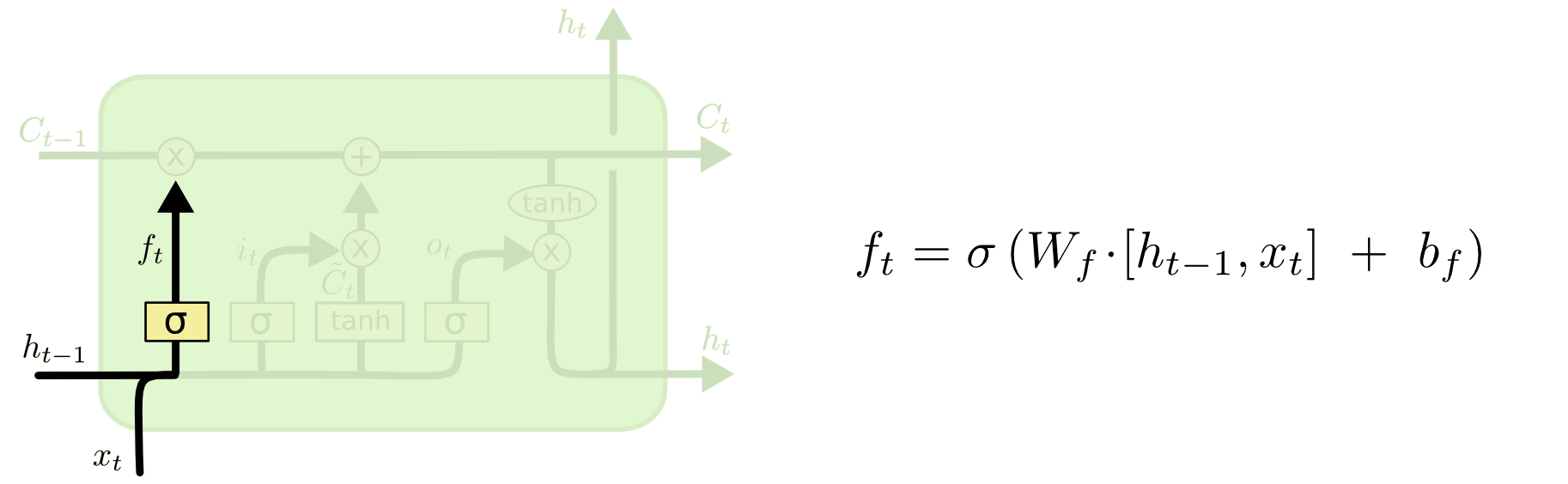
3. New information computation layers

3.1 Input gate layer

This is a trainable neural network layer which uses activation function as a sigmoid, working towards adding new information to the cell state. This layer typically scales down or filters the amount of data from the candidate list that needs to be added to the cell state.

3.2 Candidate list layer

This is another trainable neural network. But this has an activation function of $tanh$ which creates vector of new candidate values that could be added to the cell state, $\tilde{C}_t$

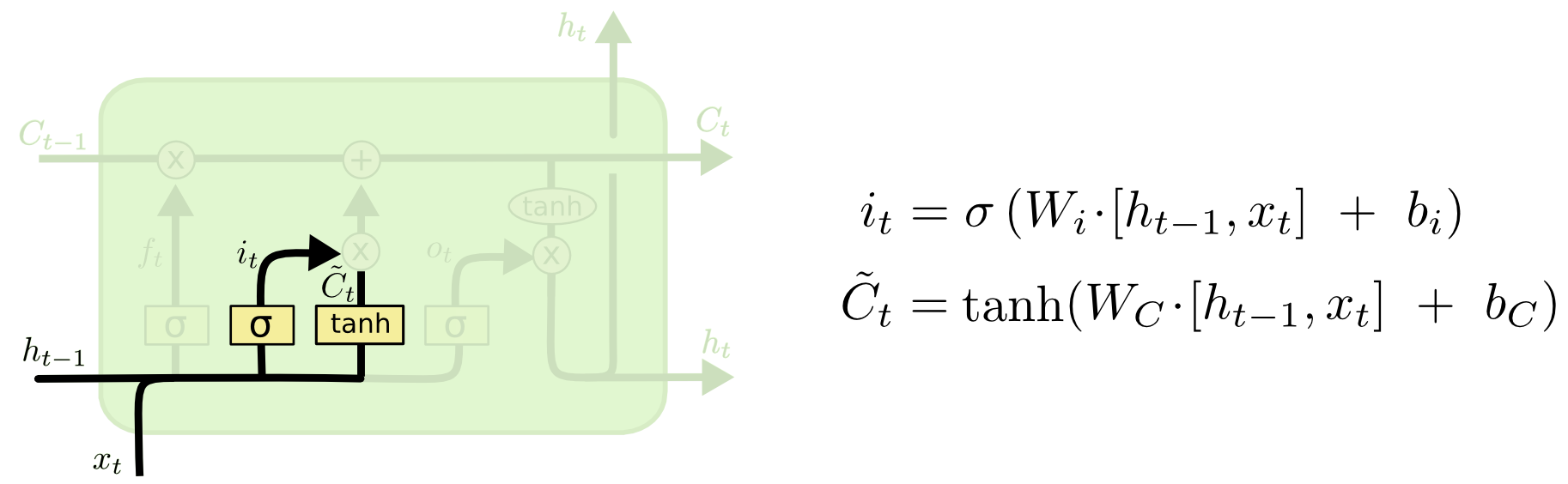
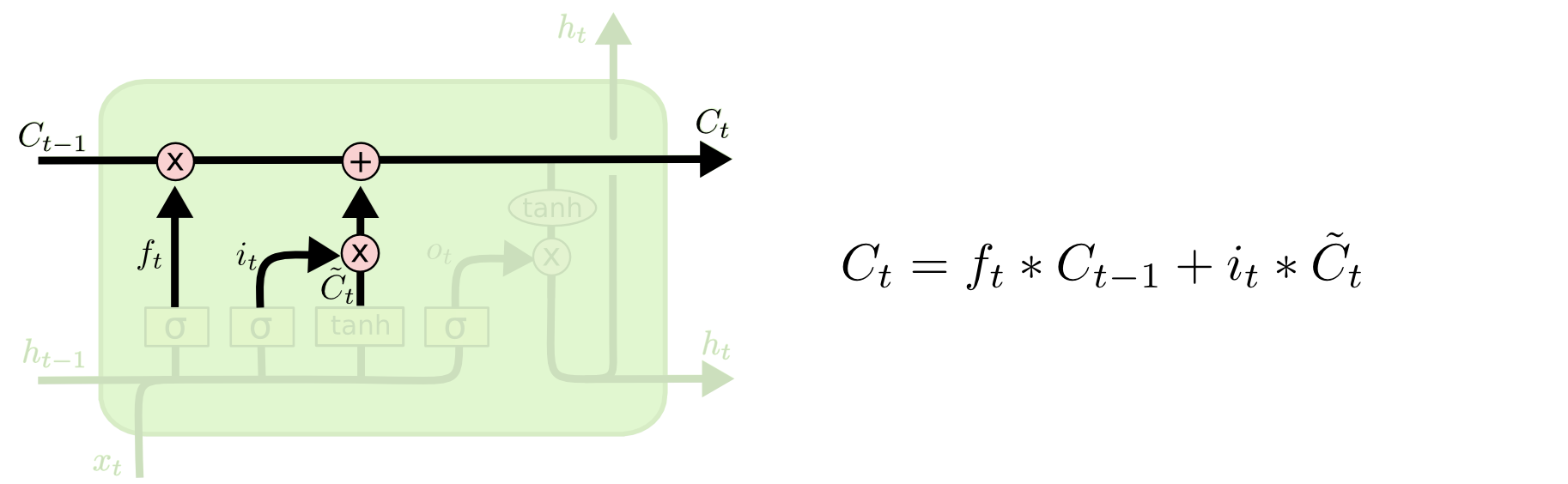
4. Update the older Cell state

It is now time to update the old cell state $C_{t−1}$ to form the new state $C_t$.

The following 3 streams of data computed above are combined with the previous cell state-

i. Forget gate layer output is point-wise multiplied with the previous cell state. This is the output from a gate, so it is multiplied to act as filter. ii. Input gate layer output is point-wise multiplied with the candidate list layer output, thereby having the gated filter applied to the candidate list. This filtered data is then added with the previous cell state..

6. Output gate layer

The output gate layer is a trainable neural network layer which uses an activation function as a sigmoid, which works as a gate, filtering concatenated current input $x_t$ and previous state $h_{t-1}$ to decide what part of the input and previous state to be exposed as output.

The cell state is passed through a $tanh$ activation function and then point-wise multiplied with the output of the output gate layer to decide what part of the cell state to be exposed as output, taking into account the previous state, current input and cell state.

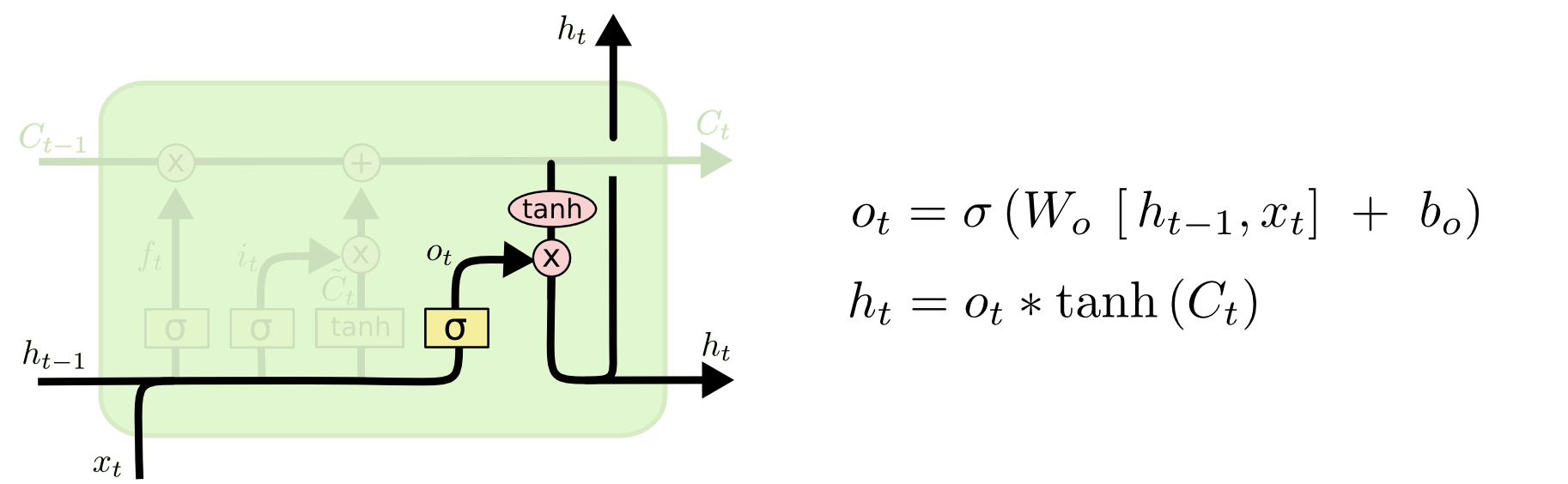
Illustration of the LSTM in work

Variations of LSTMs

1. A great comparison of various variants of LSTMs are discussed by Greff, et al. (2015).
2. Grid LSTMs by Kalchbrenner, et al. (2015) which is a 2D version of LSTMs is a huge advancement in the field of LSTMs.
3. RNNs as generative models
   1. Gregor, et al. (2015) DRAW: A Recurrent Neural Network For Image Generation
   2. Chung, et al. (2015) A Recurrent Latent Variable Model for Sequential Data
   3. Bayer, et al. (2015) Learning Stochastic Feedforward Neural Networks

Questions on LSTM

1. What is the primary purpose of gates in an LSTM (Long Short-Term Memory) network?

• To introduce non-linearity into the network
• To control the flow of information by regulating what is remembered or forgotten
• To ensure that each word has an equal impact on predictions
• To replace fully connected layers in deep learning models

2. Imagine you are training an LSTM model to predict stock prices. If an old trend from months ago is no longer relevant, which gate is primarily responsible for removing its influence?

• Forget Gate
• Input Gate
• Output Gate
• Activation Gate

3. In an LSTM, what is the primary function of the input gate?

• Selectively add new information to the cell state
• Decide which information to remove from memory
• Compute the final output at each timestep
• Store past values indefinitely

4. Suppose you are building an LSTM-based chatbot. The model has learned long-term context about a conversation, but it only needs to output the most relevant response at each step. Which gate controls what part of the memory is exposed as output?

• Forget Gate
• Input Gate
• Output Gate
• Memory Gate

5. In which of the following cases would the forget gate play the MOST crucial role?

• A sentiment analysis model that classifies a single sentence without considering previous sentences
• A weather forecasting model that continuously updates predictions based on new temperature readings
• A character-level language model that predicts the next character based only on the previous two characters
• A lookup table that always retrieves predefined values without changes